Object Mouse Trackball

Overview

The idea with trackballs is to provide an intuitive interface for complex 3D object rotation via a simple, virtual sphere - the screne space analogy to the familiar input device bearing the same name. The sphere is a good choice because it makes a good enclosure for most any object; and its surface is smooth and continuous, which is important in the generation of smooth rotations in response to smooth mouse movements. Any smooth, continuous shape, however, could be used, so long as points on its surface can be generated in a consistent way.

Having a ball

The first step in generating a trackball is defining the ball itself, which is simply a sphere at the origin

x^2 + y^2 + z^2 = r^2, where r is the radius of the sphere.

Next we would like to center our sphere on the object we would like to rotate. To do this, we can project the object's center into screen space. Let O be the projected object center. The equation for our sphere then becomes

(x - Ox)^2 + (y - Oy)^2 + z^2 = r^2.

This will place our sphere at the screen space origin, which, in OpenGL, is the lower left corner of the screen by default. We can put the origin amid screen with an additional translation of half the screen dimensions in either direction, C, giving the final form of our sphere as

(x - Cx - Ox)^2 + (y - Cy - Oy)^2 + z^2 = r^2.

Objects outside the view frustum could be culled via a sphere-frustum collision test, for example.

Of mice and manipulation

Now that we have a sphere in screen space, the rest is easy. In a nutshell, as the mouse moves over the surface of our sphere it traces out a curve. Each position on this curve from the sphere's center is a vector, and any two consecutive vectors defines (spans) a plane through the center of the sphere. The normal of this plane is our rotation axis, and the distance traveled by the mouse between any two points implicitly determines the amount of rotation.

As the mouse moves over the screen we first need to generate points on the sphere. That's a simple matter of evaluating our equation

(x - Cx - Ox)^2 + (y - Cy - Oy)^2 + z^2 = r^2, for a given mouse x and y.

But what of points outside the sphere? Frustum culling restricts us to spheres at least partially visible, but we can still generate points outside of the sphere but within the screen's extent, which would ultimately generate complex results (square roots of negative numbers). This can be seen in the explicit form of the sphere,

z(x,y) = sqrt(r^2 - (x'^2 + y'^2)), where x' and y' are the centered mouse x and y shorthands from above.

Wherever x'^2 + y'^2 > r^2, we're in deep.

One nice way to get around this unpleasantness is to use a piecewise combination of surfaces instead of just a single sphere. In this way we can switch to one surface in a region where things get nasty in another. One surface that works well in this case is the hyperbolic sheet, given by

z(x,y) = (r^2 / 2) / sqrt(x^2 + y^2).

This surface has the shape of an inverted trumpet, with the mouth piece at infinity along the z axis and the horn opening flaring out to cover the xy-plane. With the sphere nestled snugly at its opening, we can transition very smoothly from a ball to a flaring horn defined everywhere except at the origin.

Another option is to ignore points outside the sphere altogether; but bear in mind that as the mouse approaches the perimeter of the sphere, response can quickly become clumsy and unintuitive due to dz/dx and dz/dy approaching infinity near the silhouette edge.

Sphere and hyperbolic sheet

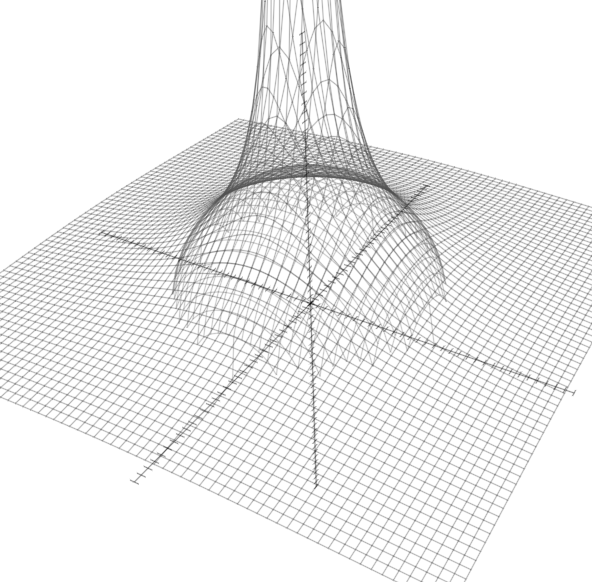
Sit and spin

So now that we can generate points for our surface anywhere on the screen, there's still the matter of generating a rotation from them. The standard way to do this is through the use of quaternions, which provide a very compact, convenient and robust representation for rotations. What makes quaternions particularly nice in this situation is the property that a normalized quaternion always represents a rotation -- as arbitrary, incremental rotations will be applied to our objects in no particular order, the importance of this property can't be overstated.

With quaternions in hand, object rotations are very straightforward. In fact, with our axis and angle from above, they're automatic. Any two consecutive (mouse) points on our surface are enough to generate two vectors, the cross product of which is the rotation axis, and the inverse cosine of the dot product of which is the angle. In pseudo code,

V1 = normalize((x1, y1, z(x1, y1)))

V2 = normalize((x2, y2, z(x2, y2)))

Axis = cross(V2, V1)

Angle = acos(dot(V2, V1))

Q = (Axis, Angle)

Q = normalize(Q)

With each incremental mouse movement we apply (accumulate) this rotation and then unitize to ensure we still have a rotation.

Numeric drift and the snap

While we can be sure our coordinate axes will remain orthogonal under rotation, due to limited floating point precision, we can't fully escape good old numeric drift in our calculations: After several arbitrary rotations, we can't be sure that we can reverse the sequence and end up with our original basis exactly. To battle these calculation creeps, it's possible to snap the rotation axes to the standard axes wherever they're very close to one another. Since a quaternion can be readily converted to and from an axis-angle representation, it's possible to first convert the quaternion to an axis-angle, snap the axis (if very close to a standard axis), angle snap, then convert the result back to a quaternion for rotation. The angle snap must be performed in lockstep with the standard axis snap, otherwise a "stair casing" effect will ensue with each incremental rotation as our object bobbles and teeters tither and hither.

Conclusion

Trackballs can provide an intuitive user interface for the interactive rotation of models in 3D.